题意:给定一个凸多面体,每个面都是透明的凸包,一束三角形的光线以某个角度照在凸多面体上,会发生透射和至多k-1次反射,求凸多面体表面被照到的面积。提交答案题…… 凸面体面数和k值都不大。
算法:
很明显就是按题目要求模拟……
3D平面的表示:点法式,一个基点和一条法线确定一个平面。
然后凸多面体的面、光线截面都可以表示为3D面上的凸包……
光线就是一条3D直线,透射、反射就是2D直线求交点、3D直线和3D平面求交点、2D反射、3D反射
光束就是一个平面上的凸包。光束在投影平面的投影:3D平面上的凸包按方向向量平移过程中与平面的交线的集合。注意光束截面可能被平面截开。如图
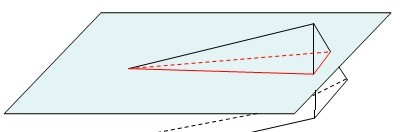
所以先把3D平面上的凸包转化为关于这个平面的相对坐标,变成2D凸包(3D点和2D点互相转换,3D凸包和2D凸包互相转换),然后求凸包所在平面和投影平面的交线,把这条交线也转成2D的,然后用它去切割凸包(半平面交),切出来的两部分就都在投影平面的一侧了,分别投影(3D直线和平面的交点),投完后得到一个凸包,再拿这个凸包和盒子上投影平面这一面的凸包(因为必须投在盒子表面的光才有效)求交(半平面交),得到投在盒子上的有效部分,作为新的反射光束截面。然后转成2D凸包存起来待用。
算总面积:对于每个盒子面的那一坨有效2D凸包求并(凸包并),可以离散化爆搞或者自适应simpson积分(需求形如x=k的直线穿过凸包的部分)。推荐simpson,非常好写,而且不会写错…… 离散爆搞会死人的……
然后使劲写就行了>_< 我写的太丑了,居然有20+KB…… 足足是nzm神犇代码量的三倍…… 果断被鄙视,就不贴了……
10.2